The Theory of NMR
Thu, Feb 29 2024
13.6 mins
Table of Contents
Introduction
If you think about it—really hard—we are all just little tiny magnets, aren’t we?
Nuclear magnetic resonance (NMR) spectroscopy is an extremely powerful tool with many interesting applications. It can be used to image tissue, identify chemical structures, map chemical taxonomy, and more!
So, what exactly is this magic?
This guide will explain the what, the
why, and the how of NMR spectroscopy!
Level 1: The Basics
The goal of NMR is to analyze a sample. Usually, this sample is dissolved in an NMR inactive solvent, and placed in an NMR tube.
Solid-state NMR, where a pure crystalline sample is analyzed without solvent is also possible. Also, an MRI machine in a hospital is just an NMR instrument—making the PATIENT the SAMPLE!
Level 2: The Theory
NMR relies on a few basic principles that are fundamental to physics and chemistry.
[N]uclear…
Every “thing” in the universe is made up of atoms. These atoms can have different properties, but they are all similar in their construction. They are all made of neutrons, protons, and electrons. An NMR active nucleus is one that has a property called spin. One such atom—and the most commonly measured—is the proton (1H). Others include 13C, 15N, and
31P! The spin causes these atoms to act like tiny bar magnets.
The NMR inactive solvents mentioned before are those which have had their protons exchanged with deuterium (2H). Deuterium is inactive because it has an even number of protons (1p+) and neutrons (1n0)! Common solvents include CDCl3, DMSO-d6, MeOD, D2O, and Acetone-d6.
With that in mind, you can measure any organic molecule!
NMR measures the presence of NMR active nuclei which are those with an odd number of particles in its nucleus.
…[M]agnetic…
So, now you have a molecule with a bunch of NMR active atoms. Now what? Well, you put them into a really strong magnetic field, of course!
An NMR instrument uses a supercooled, superconductive coil to generate an intense magnetic field called B0 in a ring around your sample. When you put NMR active nuclei into a very strong magnetic field, they begin to align themselves parallel to the magnetic field lines. The population of nuclei that align with the field is called P(α). The population that aligns against the field is called P(β).
Since the α population is aligned with the field, it is a slightly more favourable state. Thus, there is an extremely slight bias in the population in P(α). Considering that α and β populations cancel out 1-to-1 (they are aligned oppositely), there is a slight bulk magnetization with the magnetic field due to the slight bias overpopulation of P(α).
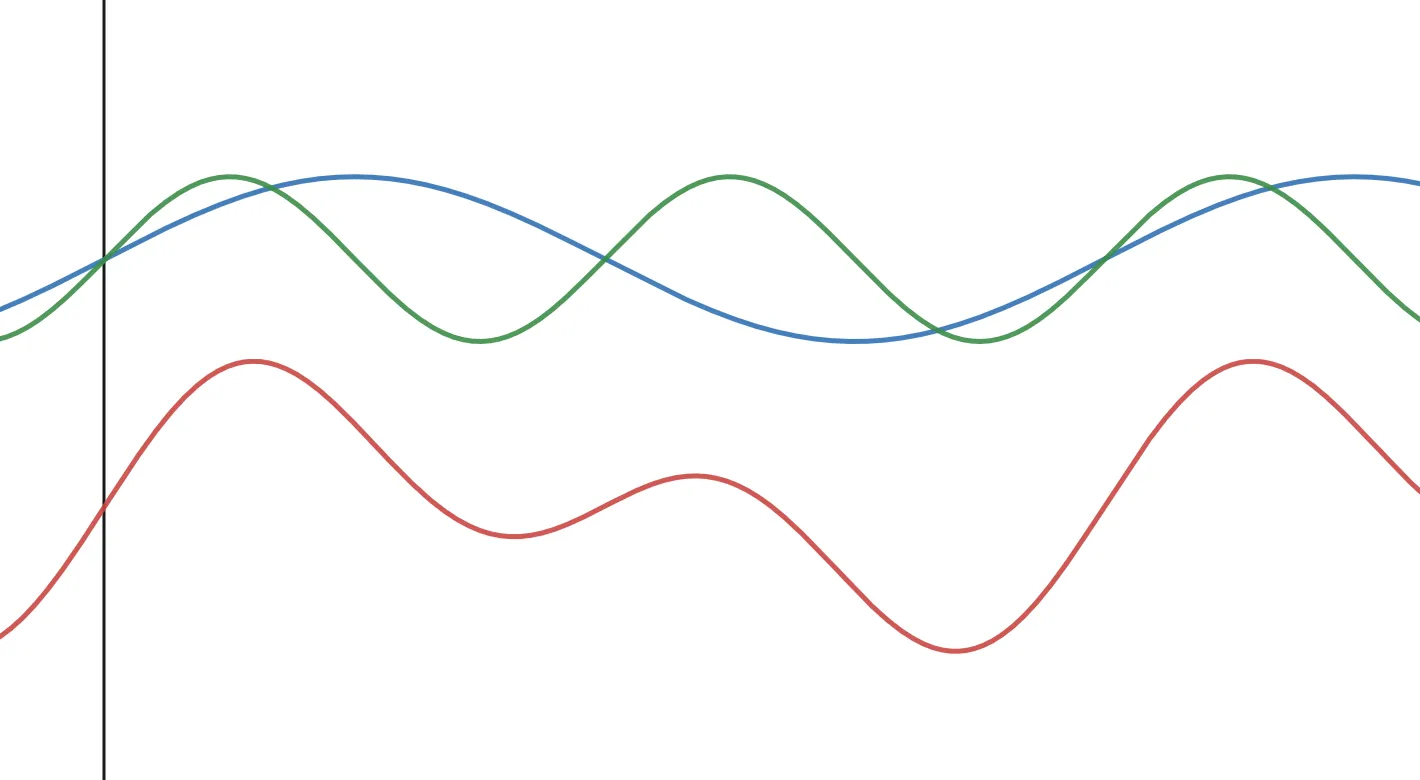
Figure 1. Left: total ensemble of spins in the sample; Right: vector of the bulk magnetization.
Conventionally, this “bulk magnetization” initially points towards the positive Z axis, or “+Z”. Note that this is different from typical 3D axes; the Z axis – not the Y axis – is the vertical one in NMR.
Putting NMR active nuclei in a magnetic field aligns them with (α) or against (β) the field lines. The population difference between the two states leads to bulk magnetization along the +Z.
…[R]esonance
A nucleus with spin also precesses. This YouTube video explains nuclear precession very well. If you don’t want to watch it, here is my best attempt at explaining it.
— TrevA nucleus with spin has angular momentum. When the bulk magnetization is aligned parallel to the magnetic field, this momentum is hard to observe. However, when the bulk magnetization is between +Z and -Z, the rotation of the nucleus is observed as precession.
This precession occurs at an angular frequency (the frequency of one full
rotation) which is characteristic for a specific nucleus at a specific magnetic
field strength. This angular frequency of precession is called the
Larmor frequency.
Level 3: The Acquisition
This one gets a little technical… bear with me!
Now that everything is aligned, we have just one problem. Nothing is really happening. Things are spinning, but we can’t see it. This is because, now that all of the atoms are either spin up or spin down, they are precessing so that their bulk magnetization is pointing along the Z axis—straight up and down.
— TrevFor visual reference, imagine looking at a spinning top from the top (and that it is spinning but locked in place). You cannot observe any change, as it all averages out pretty quick.
To actually detect something, you have to
change the direction of B0 to have a non-zero component in the
X-Y plane! That way, we can measure an oscillating current in a coil of wire. Though
not entirely accurate, you can imagine this as touching the spinning top. The top
will start to wobble, then try to return back to its original position – all while
still spinning.
There is more information about pulse sequences in this post. This post just covers the basic 1H sequence for now.
The 90° Pulse
The bulk magnetization can be moved using a radio-frequency (RF) pulse to
apply a sort of “torque” to the atoms, effectively yanking the spins in a
different direction. This is predictable, as long as we know the strength (in
Teslas) of the magnetic field. Thus, we can fine tune exactly how many
degrees we turn the vector by calculating the amount of time needed to send
the RF pulse. This is known as the pulse-width and is usually in the
microseconds. Usually, the 180° pulse is calculated first, then divided by
two to get the more common 90° pulse.
The NMR instrument that I use has a 9.4 T magnet, meaning that the pulse frequency needed to affect protons is near 400 MHz. We usually name the instruments after this frequency, so I would call it a 400 MHz NMR instrument!
When you rotate a magnet inside a coil of wire, the electrons flow in the coil with a sinusoidal period. The frequency of this wave is equal to the angular frequency I mentioned here. This is then measured as a wave in the time domain. In a molecule with many different protons in different chemical environments, this time domain signal contains the summation of all the signals. Imagine adding two sine waves together. This is important for later.

Figure 2. Two sine waves (blue & green) added together to make a compound waveform (red wave).
Inter-pulse Evolution
Evolution describes the change of atoms between events such as pulses. The time between pulses in an experiment can be the difference between having a signal and not! Without getting into TOO much detail, there are two major types of evolution. The first is chemical shift evolution and the second is called scalar evolution. Scalar evolution has a smaller effect overall, but it is important for building interesting pulse sequences!
The Rotating Frame
Evolution can be described using the rotating frame perspective. Imagine a
merry-go-Round with three people on it. You are watching this merry-go-round
spin with an angular frequency of ω from the outside perspective. The three
people on this merry-go-round represent protons that are spinning
counter-clockwise at their Larmor frequency – ω in this case. This is the
observer’s frame.
Now, here’s the kicker. The rotating frame has the same merry-go-round, but YOU
are sitting in the center, facing towards one of the three people. The
person that you are facing is now the reference frequency – again, in this
case, ω. Now you would observe that all three people are no longer moving,
as they are now moving in relation to you.
The next mental exercise considers the fact that all of these “proton” people might not experience the same magnetic field. Perhaps this is a disturbance in the homogeneity of the magnetic field, but most commonly, it is because the proton is experiencing a local magnetic field. A variety of things can cause this, but an important contributor is the local chemical and magnetic environment of the proton.
Chemical Shift Evolution
Even though the resonant frequency of a single proton is ~400 MHz in a 400 MHz instrument, that doesn’t take into account the different chemical and magnetic environments in an organic molecule. Measured in Hz, chemical shift allows us to tell proton environments from each other, as each of them (usually) show a peak with a certain amount of shift. As you now know, a higher magnetic field increases the Larmor frequency, and vice versa.
All of these shifted frequencies are present in the time domain measurement after the 90° pulse. Using a Fourier Transform, we can get the individual frequencies of the proton environments, enabling the elucidation of much more information!
So, what does it look like? Imagine that a “proton” person experiences a
greater magnetic field. Thus, its Larmor frequency – which I will now call
λ – increases, and now λ > ω. In the rotating frame, you would observe this
person as walking counter-clockwise – the direction of the merry-go-round. The
inverse is true for a lower magnetic field, where the person would be walking
clockwise – against the direction of the merry-go-round. The speed that the
person moves away from the reference person around the circle represents the
chemical shift. In other terms, it is λ - ω = δ where δ is the chemical
shift.
By subtracting the reference frequency, you essentially remove the contribution
of the large, constant magnetic field (B<sub>0</sub>) and isolate the relative
difference due to the specific chemical environment of the nucleus in the
sample.
Level 4: The Spectrum
That was all pretty abstract—sorry about that. Allow me to put this all into visual terms!
Here is an FID, or Free Induction Decay. This is what is directly measured from the instrument, in the time domain. You can think of this as taking an audio recording of a bell that you just rung. There are many different frequencies present here, all added together.
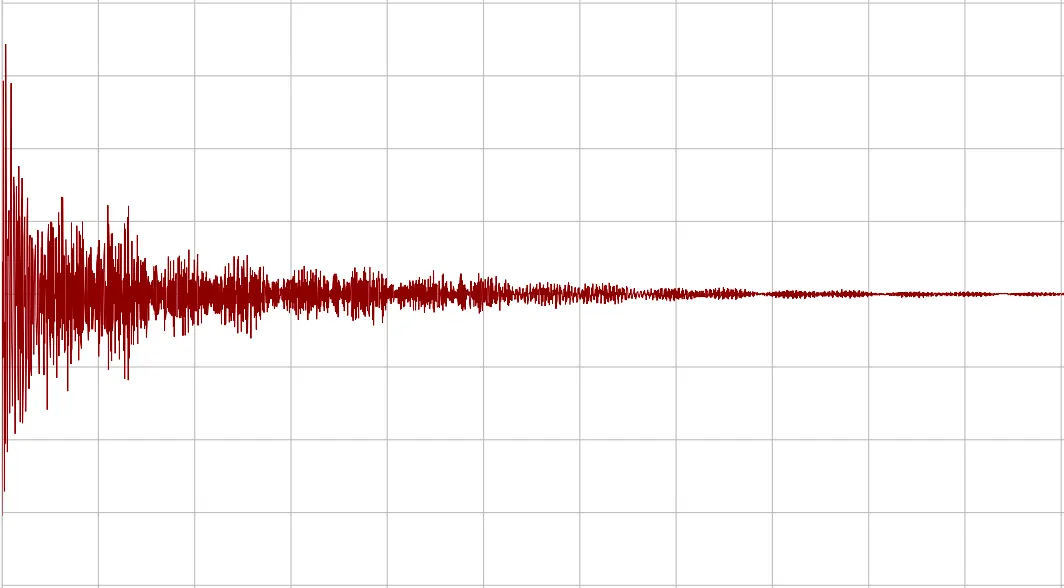
Figure 2. An unprocessed free-induction-decay spectrum.
Then, if we apply a Fourier Transform, we get this.
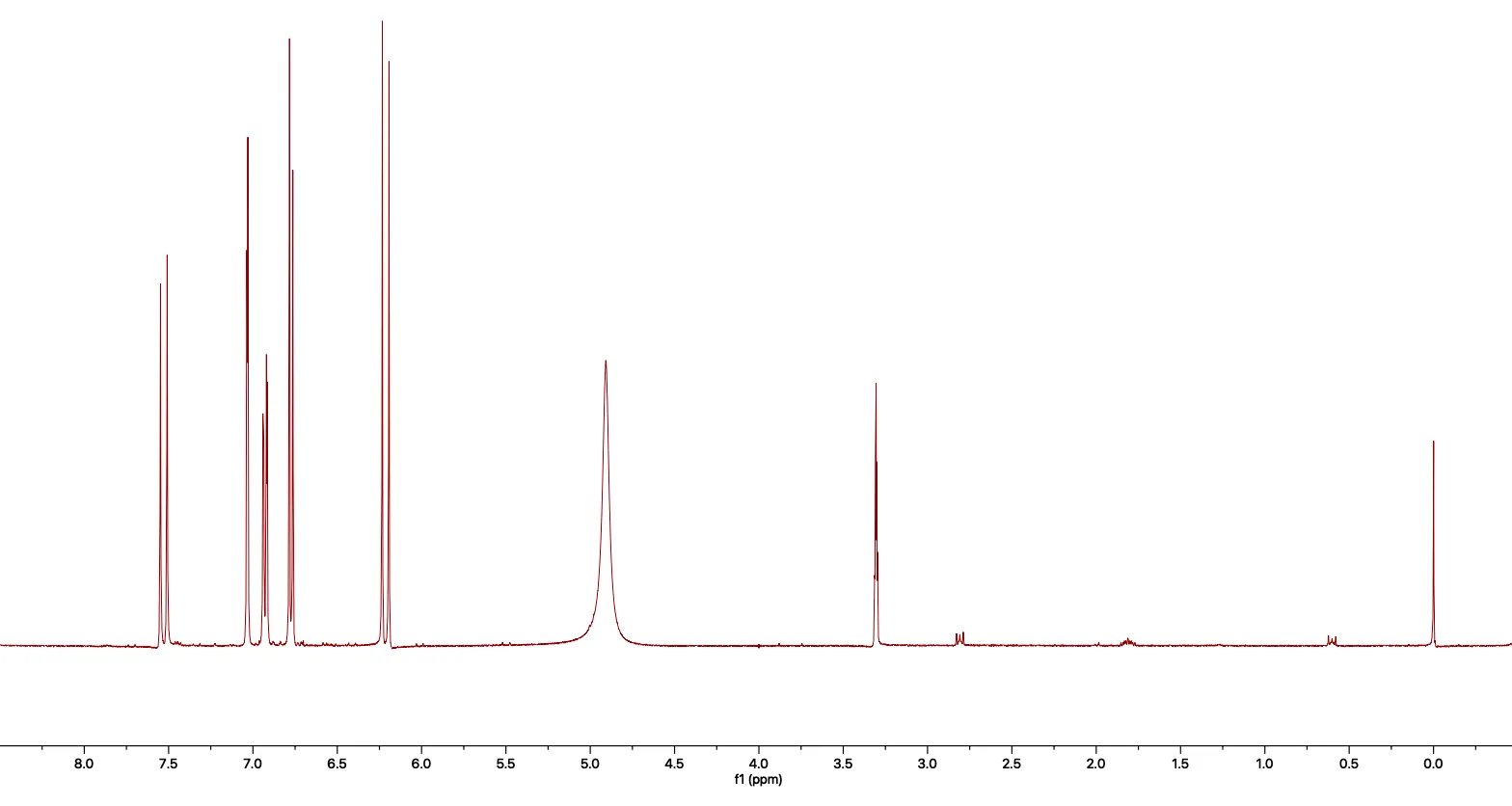
Figure 3. An FID that has been processed with the Fourier Transform.
Each of the peaks corresponds to a frequency that was measured in the original FID, giving undeniable structural information about the molecule being measured. This spectrum is one I acquired for caffeic acid.
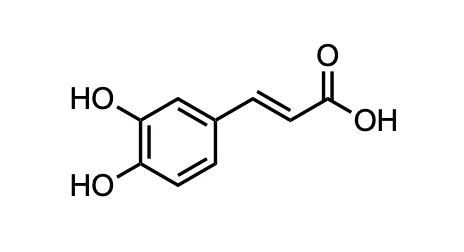
So, what do you get out of an NMR? Using the information in Figure 4 and more, you can resolve the structure, determine concentration, or even map how many different compounds are in your solution (including impurities!). NMR is extremely powerful!
I will soon write a guide on how to interpret an NMR spectrum. For now, though, this article will focus on the theory.
Level n: Other Concepts
Relaxation Pathways
There are two relaxation pathways that cause nuclei to accelerate their relaxation to the ground state.
The T1 Pathway
AKA the spin-lattice relaxation pathway – occurs when protons rotate in
relation to a 13C atom as the molecule tumbles. If the tumbling
occurs near the Larmor frequency, this induces unwanted α --> β or β --> α
transitions and returning to the ground state quicker. This is actually a
physical phenomenon!
This type of relaxation occurs mostly with medium-sized molecules (around 1000 Da).
The T2 Pathway
Random effects of tumbling molecules leads to randomized Larmor frequencies among spins, reducing coherence of the atoms. T2 relaxation occurs in the same way that Chemical Shift Evolution does.
Moreover, molecules with π-bonding have a magnetic field. If these molecules tumble slowly (over the course of acquisition window), the change in local magnetic field induces field heterogeneity within the sample. However, this doesn’t occur for quickly tumbling molecules, as the field averages out during the acquisition window.
Decoupling
The idea of decoupling is quite simple. However, I will first go over what coupling is so I can explain how to remove it!
Spin-spin J-coupling occurs because the local magnetic field produced by one
proton can affect the Larmor frequency of a neighbouring proton. Since each
proton can be either α or β, the following systems are possible:
αα, αβ, βα , or ββ. For the sake of example, we know that proton A is
spin α. On its own, it has a Larmor frequency of λ. If its neighbour
(proton B) is spin α (meaning that it is aligned WITH B0 ) it has an
additive effect on the local magnetic field. This means that the magnetic
field at proton A is higher, increasing its Larmor frequency, and thus, its
chemical shift. Moreover, the opposite is (almost) equally as likely, where
proton B is spin β. This means that the field would be subtracted from,
as it is aligned AGAINST B0 – equally subtracting from proton A’s
chemical shift.
In the spectrum, we would see proton A’s singlet split into a doublet centered at the singlet’s ppm. Furthermore, proton B would exhibit the same behaviour.
In the context of a 13C spectrum, a detected carbon is able to couple with the protons that are attached to it. So, a methyl carbon would be a quartet, a methylene would be a triplet, and so on. Recall that a RF pulse at the Larmor frequency of a proton applies a torque to it. Now, imagine that you never turn that off! The proton would just keep going around and around, constantly flipping alphas to betas and betas to alphas. If we apply a carbon pulse while continually applying a proton pulse, we can average out the effect of coupling so that each carbon peak becomes a singlet! This is the concept of decoupling.